During my semester of research, I gained an understanding of how to construct single factor models and how to predict stock prices with those models. At the start of the semester, I started by researching various financial concepts and terms, as I had no background in finance. I then went on to create a simplistic CAPM model on MATLAB. I graphically analyzed the results, and then I went on to create another model that focuses on predicting stock returns based off of expected market return. My final step was an analysis of the correlation of data that has to do with changes in federal interest rates in relation to stock returns. I am going to continue with the research this summer and see how the incorporation of the interest rate data can influence the predictive power of my models.
The purpose of this research is two-sided. The main objective is to see how the federal interest rate data affects the accuracy of stock return predictions. The secondary objective is for me to personally gain experience in financial modeling. The federal interest rate data is acquired in a very unique way by a local startup called Prattle Analytics. The company has developed a cleverly coded program that goes to websites where the notes of Federal Reserve meetings are released. The program then goes through the notes and comes up with data on the changes in bank and consumer regulations. Their goal is to sell this data to companies who will then improve their stock portfolios with their purchase.
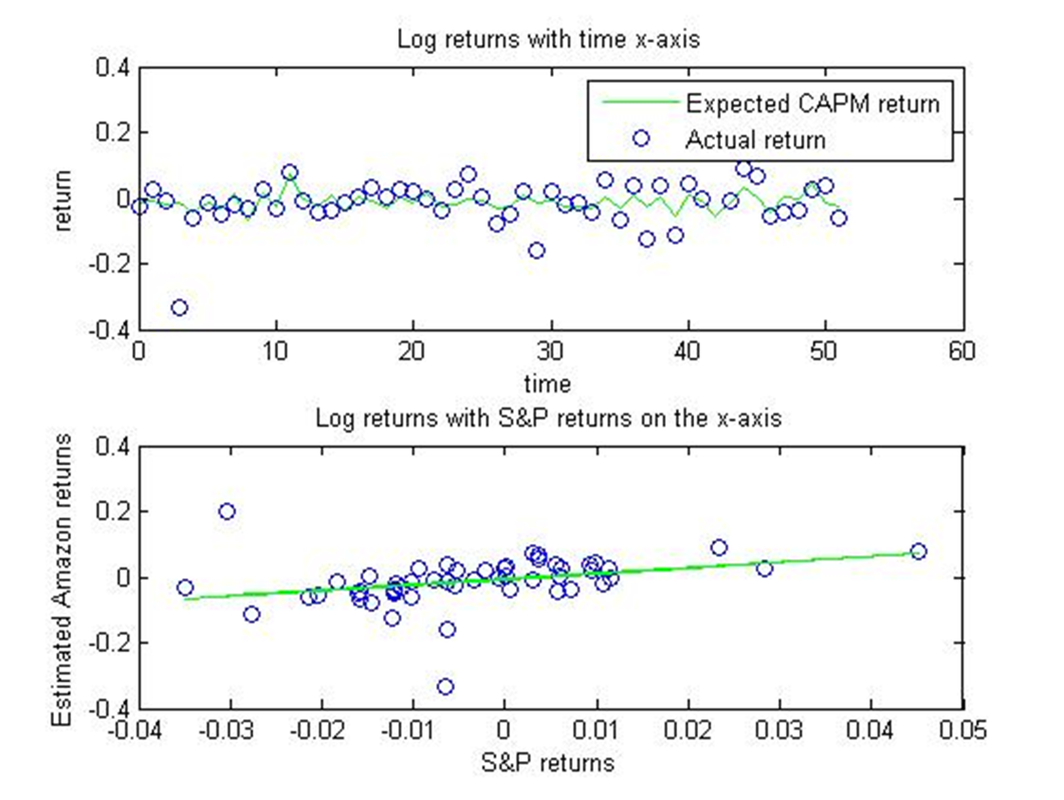
For my first simple CAPM model, I used the equation E(r)=alpha + beta*E(Rm). I used Standard and Poor as my market rate (Rm). I assumed the risk-free rate alpha, calculated by taking the average of the difference between expected returns and actual returns, to be 0. My dependent variable was the returns on Amazon stocks. All the returns are the log of the difference between the current stock price and the price from the previous day. The beta is the volatility constant of the stock. If the beta constant is greater than 1, then it is going to vary greater than the market. It will grow and shrink quicker than the market does. The beta for Amazon was approximately 1.6. These are the graphs:
For my first simple CAPM model, I used the equation E(r)=alpha + beta*E(Rm). I used Standard and Poor as my market rate (Rm). I assumed the risk-free rate alpha, calculated by taking the average of the difference between expected returns and actual returns, to be 0. My dependent variable was the returns on Amazon stocks. All the returns are the log of the difference between the current stock price and the price from the previous day. The beta is the volatility constant of the stock. If the beta constant is greater than 1, then it is going to vary greater than the market. It will grow and shrink quicker than the market does. The beta for Amazon was approximately 1.6. These are the graphs:
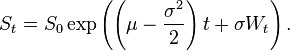
The original CAPM model was just using Standard and Poor data, not expected Standard and Poor data. In order to get a model that is based on predicting future stock returns instead of past stock returns, the market rate needs to be the expected market rate. I used a process called Geometric Brownian Motion in order to find the expected Standard and Poor returns. The formula for it is:
The stock price (St) is related linearly to the original stock price and logarithmically to the average stock price and the standard deviation of the stock.
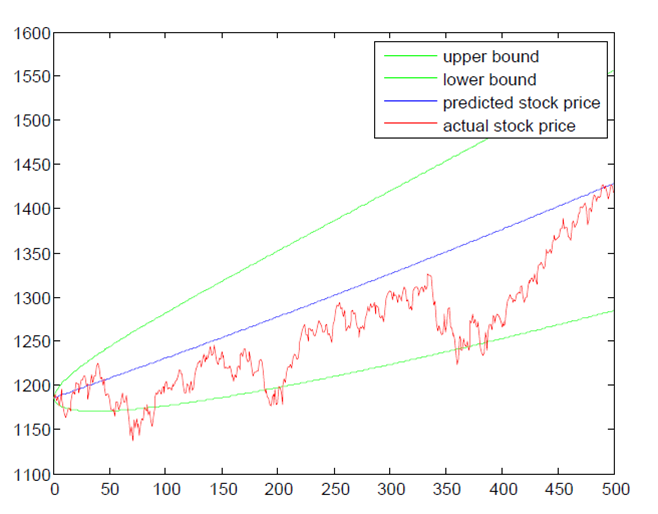
I also made an upper and lower bound confidence interval for estimated Standard and Poor returns. The graph below shows a 95% confidence interval.
The stock price (St) is related linearly to the original stock price and logarithmically to the average stock price and the standard deviation of the stock.
I also made an upper and lower bound confidence interval for estimated Standard and Poor returns. The graph below shows a 95% confidence interval.
The x axis is time, and
the y axis is Standard and Poor’s price. Even with a rather low confidence
interval, the upper bound is still very high. This means that the model’s
predictive power is not very accurate; a result of the simplistic model. There
are many other factors that could be accounted for in the model that were left
out. While adding more factors could theoretically improve its predictive
accuracy, adding additional factors can cause the model to over-fit the data.
In the real-world economy, the data being studied often has some degree of
random noise within it. Attempting to create a model with slightly inaccurate
data can cause the model to have considerable errors and diminish its
predictive power. There are downsides to both complexity and simplicity.
My next step in this project is to incorporate Prattle’s data into my Geometric Brownian Motion model and see how this affects the predictive accuracy. After looking at Prattle’s data and Standard and Poor’s returns, there seems to be a correlation between the two. It will be exciting to see it integrated into the model.
My next step in this project is to incorporate Prattle’s data into my Geometric Brownian Motion model and see how this affects the predictive accuracy. After looking at Prattle’s data and Standard and Poor’s returns, there seems to be a correlation between the two. It will be exciting to see it integrated into the model.